在概率论学习中,传统教学通常从随机试验开始,以便复习高中阶段学习的样本空间和随机事件等基础概念.通过观察频率,我们能够观察到在试验次数逐渐增多时频率呈现稳定性,这反映了统计学规律,也是概率论研究的对象.在后续学习中,组合这一概念占据着核心地位,尤其在超几何分布和二项式分布中.因此,在深入学习概率论之前,我们先来复习一下简单的概率基础知识点.1
目录
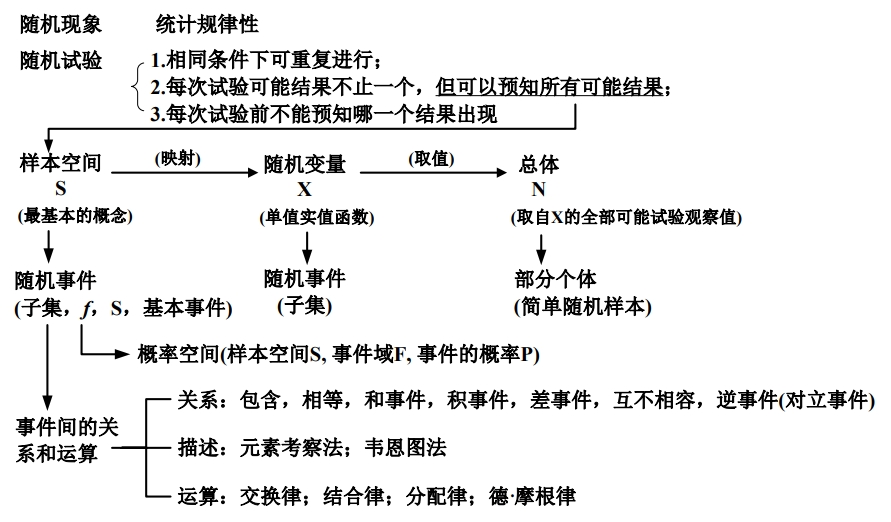
1.随机试验/样本空间/随机事件
1.1 随机试验的定义和例子
Define1:试验=做了一件事儿.随机试验=做的这件事儿需要满足一些条件.
Ex1:试验的例子
E1:扔了颗筛子
E2:抛了枚硬币
- Define2:如果一个试验满足如下三个条件,则称该试验为随机试验
(a):该试验能够在同一条件下进行多次重复
(b):该试验的可能结果不止一个,且知道这些结果都是什么
(c):进行试验之前,不知道哪个结果会发生
- Ex2:随机试验的例子(后面统一管随机试验叫做试验)
E1:扔了颗筛子,观察其出现的点数
E2:抛了枚硬币,观察其朝向
E2:抛了3次枚硬币,观察其朝向
1.2 样本空间的定义和例子
Define3:随机试验E的所有可能结果,叫做该试验的样本空间S
样本点:样本空间中的元素,也就是试验的每一个可能的结果.
Ex3:
E1:扔了一颗筛子,观察其出现的点数S1:{1,2,3,4,5,6}
E2:抛了枚硬币,观察其朝向S2:{正,反}
E2:抛了3次枚硬币,观察其朝向S3:{正正正,正正反,正反反,正反正,反正正,反正反,反反正,反反反}
1.3 随机事件的定义和例子
Define4:随机试验E的样本空间S的一个子集A,叫做随机事件A.
Ex4:
取S1的一个子集:\(A_1\) = {1,2} 或者\(A_1\) = {1,2,3} , \(A_1\) = {1,2,3,4,5,6}(它叫做必然事件) , \(A_1\) = {i}(i=1,2,3,4,5,6其中的任何一个,它叫做基本事件) , \(A_1\) = {7}(它叫做不可能事件)
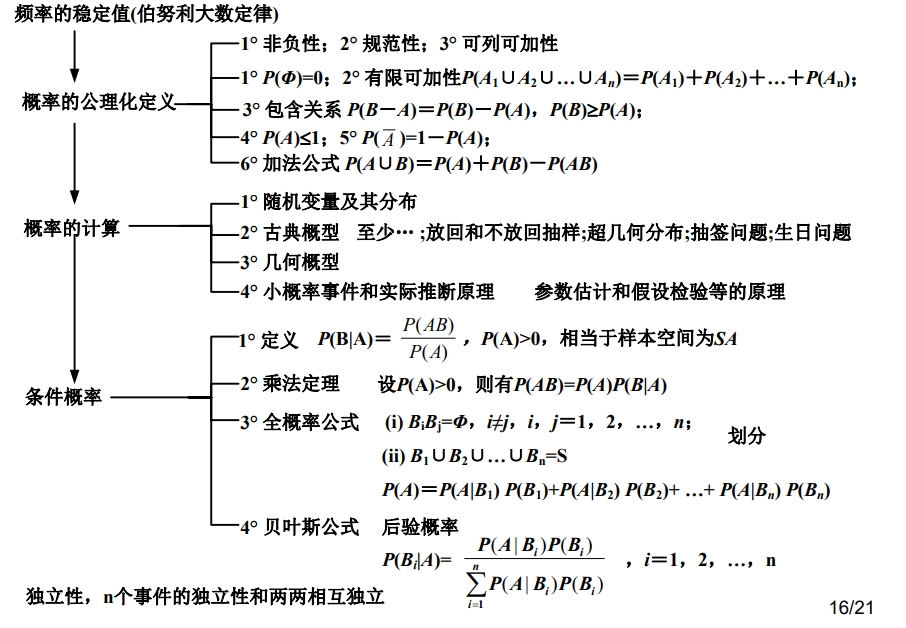
2.频率/概率/古典概型
2.1 频率/概率
为了得到概率,我们先来看一下与其密切相关的一个概念,频率
举个例子:假设在相同的条件下,我们进行了n次重复试验,其中事件A发生的次数为\(n_A\),则\(f_n(A) = \frac{n_A}{n}\)称为事件A发生的频率.频率反映了事件A发生的频繁程度2
下面看一个经典的频率试验:假设我们的试验是仍一枚硬币,观察其朝向,n是试验所重复的次数,H代表事件:正面朝上,\(f_n(A)\)代表其频率.
| 实验者 | n | \(n_H\) | \(f_n(H)\) |
|---|---|---|---|
| 摩根 | 2048 | 1061 | 0.5181 |
| 皮尔逊 | 12000 | 6019 | 0.5016 |
| 皮尔逊 | 24000 | 12012 | 0.5005 |
通过观察上面的表格,可以得到如下三个事实.2
(a) 频率有随机波动性,同样的n次试验,频率\(f_n(H)\)并不同
(b) n较小时波动很大,n增大时趋于稳定
(c) \(f_n(H)\)在0.5附近随机摆动并逐渐稳定于0.5
注意:当重复试验的次数n逐渐增大的时候,某个事件的频率逐渐趋向于稳定.有统计学家证明了当频率趋向于稳定的时候,频率=概率,即\(f_n(A)_{n \to \infty} = p(A)\),p(A)表示事件A发生的概率.
2.2 古典概型/放回抽样/不放回抽样
- Define5:若试验E满足如下两个条件,则称该试验为古典概型:
(a):该试验的样本空间只包含有限个结果
(b)该试验中的每个基本事件发生的概率相同
- Define6:一只口袋有6只球:4只白的,2只红的.从袋中取球两次,每次随机取一只,考虑两种取球方式:
(a):放回抽样:第一次取一只球,观察颜色后放回袋中,搅匀后再取一只
(b)不放回抽样:第一次取一只球不放回袋中,第二次从剩余球中再取一只
3.条件概率/全概率公式/贝叶斯公式
3.1 条件概率公式
\[\begin{equation}P(A|B) = \frac{P(AB)}{P(B)}\end{equation}\]3.2 全概率公式
假设一个试验E的样本空间为S,\(B_i\)为其事件,其中\(B_i \cap B_j = \emptyset , \forall i\neq j\),且\(\cup_{i=1}^{n} B_i = S\) ,则对于E中任何一个事件A,有如下的全概率公式.
\[\begin{equation}P(A) = P(A|B_1)P(B_1) + .... + P(A|B_n)P(B_n)\end{equation}\]3.3 贝叶斯公式
假设一个试验E的样本空间为S,\(B_i\)为其事件,其中\(B_i \cap B_j = \emptyset , \forall i\neq j\),且\(\cup_{i=1}^{n} B_i = S\) ,A为E的一个事件,则有如下贝叶斯公式:
\[\begin{equation}P(B_i|A) = \frac{P(A|B_i)P(B_i)}{\sum_{j=1}^n P(A|B_j)P(B_j)}\end{equation}\]4.事件之间的独立性
如果事件A发生的概率不影响事件B发生的概率,反之也对的话,那么称A和B相互独立!
- Define7:A和B相互独立,当且仅当:\(P(AB) = P(A)P(B),P(A)>0 , P(B)>0\)
注意:A,B相互独立与A,B互不相容不能同时成立.因为如果A,B相互独立可以得到P(AB)>0,但如果A,B互不相容得到了P(AB)=0.即相互独立\(\neq\)A与B不相交
5.总结
6.下节预告
- 数据的类型(离散型与连续型)
- 随机变量的本质意义
- 离散型随机变量及其四种分布
- 随机变量的分布函数
- 连续型随机变量及其分布
- 随机变量的函数的分布
References
知乎博主(五角场老张): https://zhuanlan.zhihu.com/p/342815857 ↩
西安电子科技大学:概率论与数理统计课件: https://web.xidian.edu.cn/lnzhu/files/20180905_163735.pdf ↩ ↩2
文档信息
- 本文作者:Zimo Li
- 本文链接:https://lizimo-n.github.io///2024/04/08/%E6%A6%82%E7%8E%87%E8%AE%BA-%E5%9F%BA%E6%9C%AC%E6%A6%82%E5%BF%B5/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)