小李的博客

第四节：通俗理解分布函数、概率密度函数。

2024/04/12 概率论 共 3202 字，约 10 分钟

我们上一节讲解了什么是分布以及三种常见的离散分布，那么本节主要想讲解一下什么是分布函数，它与分布有什么关联，为什么要有这个分布函数呢？什么是密度函数呢？。(这一节我理解的还不是特别透彻，我后续还会继续理解，所以这一节仅供参考，不对的地方请大家多多指正)

1.分布函数

1.1 回顾什么叫分布

 我们上节课说到：分布(概率分布)在离散情况下表示的是某个点的概率值,在连续情况下表示的是某个区间的概率值

 我们缕一下思路，正常情况下，我是怎么得到这些概率值的呢？首先我应该做大量的实验，然后把大量的实验结果转换为概率，就得到了所谓的分布。或者是你知道这个随机变量X服从某个分布，然后我们能求得x对应的概率值。

 举个例子，我现在知道离散随机变量X服从二项分布，X的可能取值为：0，1，2，则我可以得到X的分布，如下：

X012
P$$ (1-p)^2 $$$$ 2p(1-p) $$$$ p^2 $$

1.2 引入分布函数

 概率论的目的就是想研究随机变量X的统计规律，那你看上面的概率分布表，我现在只有3个取值，能描述的信息就比较少。那么为了更好的掌握X的统计规律，我就需要掌握X取各种值的概率。换句话说：我现在为了掌握X的统计规律，不仅要知道X在每个取值处的概率\(p(X=x_i)\)，我还要知道其他地方的概率。

 那其他地方的概率可以描述为：

\[P(a< X \leq b) , p(X>c) , p(X\leq c)\]

 而

\[P(a< X\leq b) = p(X\leq b) - p(X\leq a)，p(X>c) = 1-p(X\leq c)\]

 因此，对于任意的实数x，我只需要研究\({X\leq x}\)的概率就可以了，其余的我都可以由它算出来！这就是分布函数的起源，说白了，分布函数的核心就是想算各种地方的概率。

 我如果知道了X在取值点处的概率分布，那我就可以求其分布函数，从而求得在任何地方的概率值！下面来看分布函数的公式定义吧~

  • Define1：设X是一个随机变量，x是任意的实数，则\(F(x) = p(X\leq x)\)称之为X的分布函数

2.离散数据的分布函数与分布之间的关系

 我们如果知道了离散随机变量X在每个取值点处的分布(概率)，那我可以求得它的分布函数，从而我就可以求X在任意地方的概率值了。

  • 离散随机变量X的分布函数：假设离散随机变量X的所有可能取值为：\(x_1,x_2,...,x_n\)，设\(p(X=x_i) = p(x_i) = p_i\)，则X的分布函数如下：
\[\begin{equation} F(x) = \begin{cases} 0 & , -\infty < x < x_1 \\ p_1 & , x_1 \leq x < x_2 \\ p_1 + p_2 & , x_2 \leq x < x_3 \\ \vdots \\ \sum_{i=1}^n p_i = 1 & , x \geq x_n \end{cases} \end{equation}\]

 okok，那么我们下面就举一个小小的例子来算算吧~

  • Ex：假设随机变量X的取值为-1，2，3，且p(X=-1) = 0.25 , p(X=2) = 0.5 , P(X=3) = 0.25，求：

    (1)X的分布函数     (2)\(p(X\leq 0.5) , p(1.5<X\leq 2.5)\)

    解：现在是知道了随机变量的分布，我们要求分布函数。根据如上公式可以得到：

\[\begin{equation} F(x) = \begin{cases} 0 & , -\infty < x < -1 \\ 0.25 & , -1 \leq x < 2 \\ 0.25 + 0.5 & , 2 \leq x < 3 \\ 1 & , x \geq 3 \end{cases} \end{equation}\]

    则：

\[p(X\leq 0.5) = F(0.5) = 0.25\] \[p(1.5<X\leq 2.5) = p(X\leq 2.5) - p(X\leq 1.5) = F(2.5) - F(1.5) = 0.75-0.25=0.5\]

    那么现在反过来，如果我们知道了X的分布函数，我们可以试着求X的分布，即求p(X=-1),p(X=2),p(X=3)

\[p(X=-1) = p(X\leq -1) = F(-1) = 0.25\] \[p(X=2) = p(X\leq 2) - p(X=-1) = p(X\leq 2) - p(X\leq -1) = F(2) - F(-1) = 0.75-0.25=0.5\] \[p(X=3) = p(X\leq 3) - p(X\leq 2) = F(3) - F(2) = 1-0.75=0.25\]

    通过这个例子，如果你将F(x)的图像画出来，你会发现，它的图形是跳跃的分段函数，在每个取值点（比如X=-1，X=2，X=3）处都是不连续的。这并不是个特例，事实上：如果随机变量为离散的，那么其分布函数一定是右连续的跳跃函数

    你可能也发现了，对于离散的随机变量，我们求出来\(p(1.5<X\leq 2.5)\)也没有什么意义，事实确实是这样，在离散随机变量中，我们更关心的是X的分布，而不是它的分布函数！

3. 概率密度函数

 我们在第二节：随机变量已经描述了什么是连续型随机变量，那么这一小节，我们就来看看神秘的概率密度函数！

 引用书中的一个例子：加工螺丝的直径的测量值是一个随机变量X，如果我们一个接一个的测量其直径，把测量值x一个接一个的放到数轴上去，当累积了很多测量值x的时候，就形成了长度上的频率，如下图1。为了使得这个图形得以稳定，我们把纵轴由“单位长度上的频数”改为“单位长度上的频率”，如下图2，此时可以描述出一个曲线。由于频率的稳定性，随着测量值x越来越多，其纵坐标上的一个点就是概率，如下图3，这条曲线是光滑的曲线，此时图3纵坐标就是一点上的概率密度。这条曲线所表示的函数p(x)成为概率密度函数！

p3

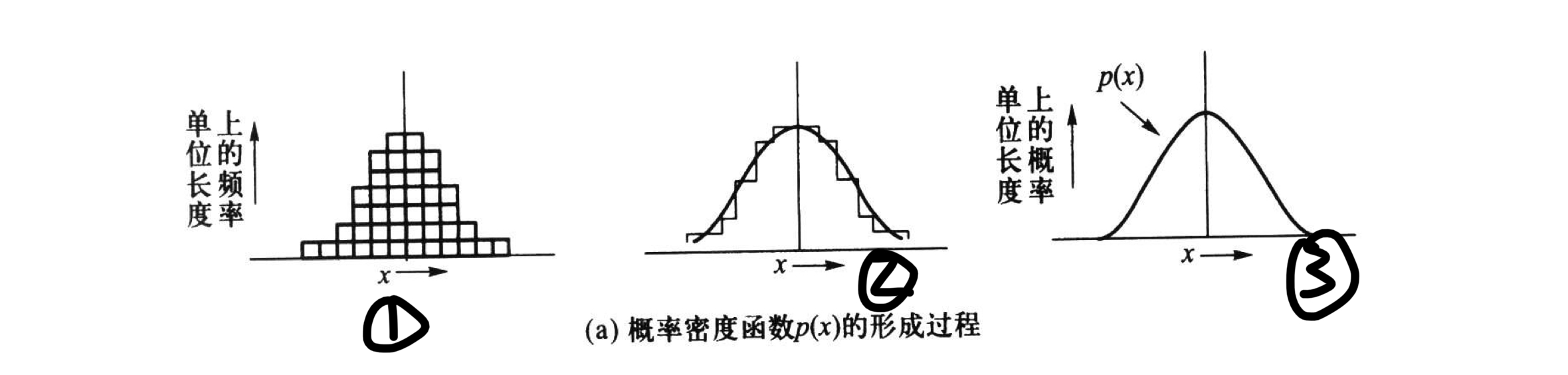
注意：这里面的p(x)和我们离散时候的p(x_i)可不是一个东西，这里面的p(x)表示的是一个函数，而离散时候的p(x_i)表示的是一个点的概率分布

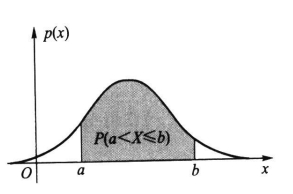
 那么在坐标轴上有了这条曲线，我们最想做的事情就是求概率嘛，那如何求对应区间的概率呢？我们下面给出连续随机变量X在区间(a,b]上的概率分布公式

  • Define3：\(p(a<X\leq b) = \int_{a}^bp(x)dx\)

 事实上求它的概率分布就是在求其密度函数的积分，也就是求面积嘛！

p4

 我们在最开始就说了，如果我们现在知道了X的分布，然后我们能把每一个连续小区间的概率分布求出来，但是我现在想求任何区间的概率分布，怎么办呢？那就整上所谓的分布函数呗!(再次强调，分布函数的本质就是想求任何地方的概率，它只是求概率的一个桥梁)

  • Define4：设X是连续型随机变量，对于任意的实数x，如果有非负可积的函数p，则\(F(x) = \int_{-\infty}^{x} p(t)dt\)为X的分布函数，p叫做X的概率密度函数

 由微积分的知识我们可以很容易的知道F(x)是一个连续函数。

 我们回想一下，如果随机变量X是离散的，假设X的可能取值为：\(x_1,...,x_n\)，则\(p(X=x_i)\neq 0\)。那现在问题是如果X是连续型随机变量，那X在某一点的概率值是多少呢？其实都不用公式推导，你仔细想一下，我们说连续随机变量求概率等价于求面积，那在一个区间上你肯定能求面积，但是在一个点上，你怎么求面积呢？所以在一个点处的面积肯定是0呀，即X在某一点的概率值是0！

4.注意

我们虽然讲了很多关于分布、分布函数的事情，但是通常情况下，如果X是一个离散随机变量，说X的分布一般是指其分布列，如果X是一个连续随机变量，说X的分布一般是指其概率密度函数！

 所以，我们可以将分布列和概率密度函数看成一个东西，只不过是两种不同数据类型的表达~

5.下节预告

  • 常见的连续型分布

  • 通俗理解一维变量的期望和方差

文档信息

Search

    Table of Contents